Analysis of the actual results of a Steinway L which have been provided by Jason Kanter (second table):Actual beat rates for major thirds (difference between the frequency of the 4th partial of the upper note and the frequency of the 5th partial of the lower note):
A2-C#3 = 553.97 − 549.32 = 4.65 beats per second.
C#3-F3 = 698.46 − 693.04 = 5.42 beats per second.
F3-A3 = 881.11 − 873.89 = 7.22 beats per second.
A3-C#4 = 1111.54 − 1102.83 = 8.71 beats per second.
Actual beat ratios:
A2-C#3-F3 = 5.42 / 4.65 = 1.17.
C#3-F3-A3 = 7.22 / 5.42 = 1.33.
F3-A3-C#4 = 8.71 / 7.22 = 1.21.
Analysis of the theoretical values which have been provided by Jason Kanter (first table): Theoretical beat rates for equally tempered major thirds (difference between the frequency of the 4th partial of the upper note and the frequency of the 5th partial of the lower note):
A2-C#3 = 554.37 − 550.00 = 4.37 beats per second.
C#3-F3 = 698.46 − 692.96 = 5.50 beats per second.
F3-A3 = 880.00 − 873.07 = 6.93 beats per second.
A3-C#4 = 1108.73 − 1100.00 = 8.73 beats per second.
Theoretical beat ratios:
A2-C#3-F3 = 5.50 / 4.37 = 1.26.
C#3-F3-A3 = 6.93 / 5.50 = 1.26.
F3-A3-C#4 = 8.73 / 6.93 = 1.26.
My comments:The actual beat ratios and the actual beats per second are close to the theoretical beat ratios and the theoretical beats per second. Therefore, this could mean that a good approximation of equal temperament has been produced.
I think two pairs of equally beating contiguous major thirds could be produced by lowering only F3 on the Steinway L. However, I think it could be difficult to ascertain how much F3 should be lowered due to the unpredictability of the actual results.
------------------------------
Roshan Kakiya
------------------------------
Original Message:
Sent: 06-05-2019 20:39
From: Ed Sutton
Subject: A Request for Roshan Kakiya
Roshan-
Just compare the A-C# thirds on the real world piano.
A2-C#3 = 4.65 bps
A3-C#4 = 8.71 bps
If you remeasured the notes on the piano, you would probably get slightly different readings.
This is the fuzziness we work with. The world doesn't have the unlimited decimal point precision of mathematics.
In tuning we use many rules of thumb that are close enough for our needs.
Perhaps you can find some spectrographs of piano sound over time, showing real beat rates can vary in just a few seconds.
------------------------------
Ed Sutton
ed440@me.com
(980) 254-7413
Original Message:
Sent: 06-05-2019 19:52
From: Roshan Kakiya
Subject: A Request for Roshan Kakiya
Thank you for providing these tables, Jason.
The first table contains the theoretical frequencies for twelve tones to the pure octave equal temperament. It confirms that my calculations for A2, C#3, F#3, A3 and C#4 are correct. Every major third has a theoretical size of 400 cents.
However, Ed's aim is to create two pairs of equally beating contiguous major thirds rather than two pairs of equally tempered contiguous major thirds.
I have confirmed, by performing calculations, that this can be achieved theoretically to a high degree of accuracy by lowering F3 so that the theoretical size in cents of C#3-F3 decreases from 400 cents to 396.888019142191 cents and the theoretical frequency of F3 decreases from 174.61 Hz to 174.30 Hz.
The first table can be modified by changing the frequency of F3 from 174.61 Hz to 174.30 Hz to account for Ed's aim.
This is Ed's aim:
"Sequentially, the four thirds should beat 4:4:8:8".
This ratio can also be expressed in the following way (beat rate of upper third divided by beat rate of lower third):
A2-C#3-F3 = 4 / 4 = 1.
C#3-F3-A3 = = 8 / 4 = 2.
F3-A3-C#4 = 8 / 8 = 1.
My analysis produces, to a high degree of accuracy, exactly the same results if the ratios are converted to whole numbers:
A2-C#3-F3 = 4.25 / 4.37 = 0.97 = 1.
C#3-F3-A3 = 8.50 / 4.25 = 2.00 = 2.
F3-A3-C#4 = 8.73 / 8.50 = 1.03 = 1.
A quick test for two pairs of equally beating contiguous major thirds (lower third : upper third):
Beat ratio of A2-C#3-F3 = 4:4 = 1:1.
Beat ratio of C#3-F3-A3 = 4:8 = 1:2.
Beat ratio of F3-A3-C#4 = 8:8 = 1:1.
I have no tuning experience so I cannot provide the actual results, which include inharmonicity, of a Steinway L. I do not know how much F3 should be lowered to cause A2-C#3-F3 to beat equally and F3-A3-C#4 to beat equally on a Steinway L.
I have performed a theoretical review, which does not account for inharmonicity, of all the information that I have posted on this thread. It is correct because I have mathematically fulfilled Ed's aim.
However, I cannot perform a practical review, which does account for inharmonicity, of it since I cannot tune a piano.
------------------------------
Roshan Kakiya
Original Message:
Sent: 06-05-2019 16:18
From: Jason Kanter
Subject: A Request for Roshan Kakiya
Here is some useful raw data to use while analyzing real-world beat rates.
Taking just the range A2 through C#4, and the partials 1, 2, 3, 4, 5, 6, and 8, you get the following set of frequencies simply with pure math, which is what Roshan has been using:
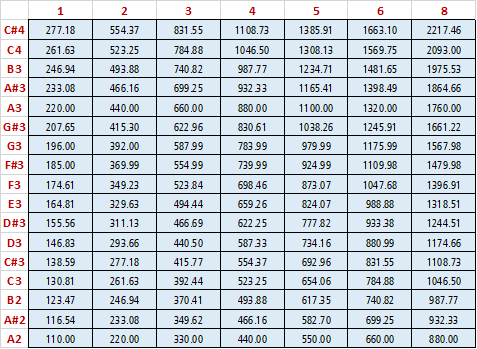However the actuality of course includes the effect of inharmonicity. Here are the actuals from a Steinway L that I recently tuned. (This data is extracted from Verituner.)
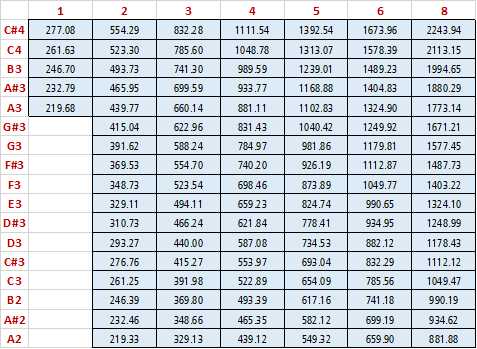Having assembled this, one can calculate what the actual beat rates are. I may do that, or perhaps some of you will find another use for this interesting set of data.
------------------------------
Jason Kanter
Lynnwood WA
425-830-1561
Original Message:
Sent: 06-03-2019 17:32
From: Roshan Kakiya
Subject: A Request for Roshan Kakiya
Definition of validity:
"The quality of being logically or factually sound".
Source: https://en.oxforddictionaries.com/definition/validity
------------------------------
Roshan Kakiya
Original Message:
Sent: 06-02-2019 19:48
From: Roshan Kakiya
Subject: A Request for Roshan Kakiya
I have already reviewed all the information that I have posted on this thread.
I want someone else to review it as well to assess its validity.
------------------------------
Roshan Kakiya
Original Message:
Sent: 06-02-2019 17:32
From: Jason Kanter
Subject: A Request for Roshan Kakiya
You can review yourself using the attached spreadsheet and studying the "panoply" page.
| || ||| || ||| || ||| || ||| || ||| || ||| || |||
jason's cell 425 830 1561
Original Message------
I highly recommend peer reviewing all the information that I have posted on this thread.
------------------------------
Roshan Kakiya
Original Message:
Sent: 06-02-2019 08:50
From: Roshan Kakiya
Subject: A Request for Roshan Kakiya
"...an estimate of 4.3 bps is good for the A2-C#3 third in many pianos."
If A4 = 440 Hz is the point of reference, the beat rate of A2-C#3, an equal-tempered major third, would be approximately 4.37 beats per second, as shown on one of my previous posts. Therefore, an estimate of 4.4 beats per second is likely to be more accurate.
"...setting F3 involves tuning a little low, then a little high, then lightly settling to the exact pitch...".
This is the same problem that I had encountered when I was performing my calculations. This practical problem probably exists because it is a theoretical problem. I was continuously decreasing and increasing the size in cents of F3 to find an excellent approximation to solve this problem.
The solution: the beat ratio of A2-C#3-F3 and the beat ratio of F3-A3-C#4 should be as close as possible to 1 to create two pairs of equally beating contiguous major thirds. This can be achieved by ensuring the deviation of the beat ratio from 1 is the same for A2-C#3-F3 and F3-A3-C#4. The aim is to flatten F3 to make C#3-F3 beat slower and F3-A3 beat faster. This should lead to the production of an equal-tempered A2-C#3, a less than equal-tempered C#3-F3, a more than equal-tempered F3-A3 and an equal-tempered A3-C#4. I have created a special major third via trial and error that specifically solves this problem:
Special Tempered Major Third = 396.888019142191 cents.
Frequencies:
A2 = 110 Hz.
C#3 = 138.59 Hz.
F3 = 174.30 Hz.
A3 = 220 Hz.
C#4 = 277.18 Hz.
Cents and beat rates:
A2-C#3 = 400.00 cents = 4.37 beats per second.
C#3-F3 = 396.888019142191 cents = 4.25 beats per second.
F3-A3 = 403.111980857809 cents = 8.50 beats per second.
A3-C#4 = 400.00 cents = 8.73 beats per second.
Beat ratios:
A2-C#3-F3 = 4.25 / 4.37 = 0.97.
C#3-F3-A3 = 8.50 / 4.25 = 2.00.
F3-A3-C#4 = 8.73 / 8.50 = 1.03.
Deviation of beat ratios from 1:
A2-C#3-F3 = 0.97 − 1 = −0.03.
C#3-F3-A3 = 2.00 − 1 = +1.00.
F3-A3-C#4 = 1.03 − 1 = +0.03.
------------------------------
Roshan Kakiya
Original Message:
Sent: 06-02-2019 06:57
From: Ed Sutton
Subject: A Request for Roshan Kakiya
Dan Levitan gives the common approach to tuning a stack of major thirds.
It requires educated guessing and accurate hearing of fast thirds at the top.
In my April tuning article I present a different approach.
Al Sanderson had suggested expanding the stack to two octaves so that issues that appear when the lower thirds and octaves are tuned are heard and dealt with before tuning more notes.
David Sumrall invented and Jack Stebbins has taught a method to speed up the process of estimating and refining small stack.
Jim Coleman suggested beginning the thirds at the low end, where they are slower-beating and easier to hear, and that an estimate of 4.3 bps is good for the A2sC#3 third in many pianos.
The April article combines all these discoveries into a simple sequence that makes it easy and fast to place and confirm seven guidepost notes across the midrange. These notes provide extended reference intervals for tuning the rest of the temperament. Knowing how to confirm them removes much of the trial-and-error from aural temperament tuning.
In doing this I stumbled onto the rule-of-thumb I asked Roshan and Dan to check mathematically. Since setting F3 involves tuning a little low, then a little high, then lightly settling to the exact pitch, the confirmation of the C# estimate can be added with no disturbance to the sequence.
(The tuning articles are a continuing series in the Piano Technicians Journal. We are also publishing an extended series of core competency repair articles by Bill Monroe.The Journal is a member benefit, or you can contact the Home Office and subscribe.)
------------------------------
Ed Sutton
ed440@me.com
(980) 254-7413
Original Message:
Sent: 06-02-2019 01:12
From: Cobrun Sells
Subject: A Request for Roshan Kakiya
Granted I haven't yet read this entire thread, but I did see in Levitan's book the attempt at fixating a smooth progression between F3 A3 C#4 F4 A4.
Mathematically I'm not sure how it'd look on paper, but having learned:
1. Tune A4 from source
2. Tune A3 from A4
3. Estimate F3 from A3
4. Tune F4 from F3
5. Tune C#4 so that the major 3rds F3A3 A3C#4 C#4F4 progress evenly
6. Retune F4 so that A3C#4 C#4F4 F4A4 progress evenly
7. Retune F3 to F4
8. Repeat steps 5-7 until F3A3C#4F4A4 skeleton of major 3rds progresses evenly
------------------------------
Cobrun Sells
cobrun94@yahoo.com
Original Message:
Sent: 06-01-2019 21:46
From: Ed Sutton
Subject: A Request for Roshan Kakiya
Roshan-
Thank you!
Dan Levitan did somewhat similar calculations and reached a similar conclusion.
Practically, the theorem is true, especially given the inherent irregularities and complications of piano sound.
But mathematically, it's a little bit less that perfect.
In fact, I accidentally noticed it when experimenting with ways to tune stacks of thirds from A2-A3-A4.
Only after a long time on a long road trip did I begin thinking about a conceptual structure for my experience.
------------------------------
Ed Sutton
ed440@me.com
(980) 254-7413
Original Message:
Sent: 06-01-2019 21:13
From: Roshan Kakiya
Subject: A Request for Roshan Kakiya
I think the difference between the 4th partial of the upper note and the 5th partial of the lower note of the major third determines its beat rate in beats per second. I will test this theory.
Frequencies for equal-tempered major thirds (A4 = 440 Hz):
A2 = 440 Hz × 1/4 = 110 Hz.
C#3 = 110 Hz × 2 400 / 1200 = 138.59 Hz.
F3 = 110 Hz × 2 800 / 1200 = 174.61 Hz.
A3 = 110 Hz × 2 1200 / 1200 = 220 Hz.
C#4 = 110 Hz × 2 1600 / 1200 = 277.18 Hz.
Beat rates for equal-tempered major thirds (difference between the frequency of the 4th partial of the upper note and the frequency of the 5th partial of the lower note):
A2-C#3 = 110 Hz × 2 400 / 1200 × 4 − 110 Hz × 5 = 4.37 beats per second. Your estimate, 4.3 beats per second, is rather close to this.
C#3-F3 = 110 Hz × 2 800 / 1200 × 4 − 110 Hz × 2 400 / 1200 × 5 = 5.50 beats per second.
F3-A3 = 110 Hz × 2 1200 / 1200 × 4 − 110 Hz × 2 800 / 1200 × 5 = 6.93 beats per second.
A3-C#4 = 110 Hz × 2 1600 / 1200 × 4 − 110 Hz × 2 1200 / 1200 × 5 = 8.73 beats per second.
"My claim is that if the C#s are properly tempered for equal temperament, when one pair is altered to beat equally, the other pair will also beat equally. In this example the C#-F third beats slower than it would in equal temperament, and the F-A third beats faster."
This idea seems to be correct. If C#3-F3 is flattened, it will beat slower. If F3-A3 is sharpened, it will beat faster.
I have manually found the value of a special major third via trial and error that is needed to produce equal beating major thirds:
Special Tempered Major Third = 396.888019142191 cents.
Frequencies for equal beating major thirds (A4 = 440 Hz):
A2 = 440 Hz × 1/4 = 110 Hz.
C#3 = 110 Hz × 2 400 / 1200 = 138.59 Hz.
F3 = 110 Hz × 2 (400 + 396.888019142191) / 1200 = 174.30 Hz.
A3 = 110 Hz × 2 1200 / 1200 = 220 Hz.
C#4 = 110 Hz × 2 1600 / 1200 = 277.18 Hz.
Beat rates for equal beating major thirds (difference between the frequency of the 4th partial of the upper note and the frequency of the 5th partial of the lower note):
A2-C#3 = 110 Hz × 2 400 / 1200 × 4 − 110 Hz × 5 = 4.37 beats per second.
C#3-F3 = 110 Hz × 2 (400 + 396.888019142191) / 1200 × 4 − 110 Hz × 2 400 / 1200 × 5 = 4.25 beats per second.
F3-A3 = 110 Hz × 2 1200 / 1200 × 4 − 110 Hz × 2 (400 + 396.888019142191) / 1200 × 5 = 8.50 beats per second.
A3-C#4 = 110 Hz × 2 1600 / 1200 × 4 − 110 Hz × 2 1200 / 1200 × 5 = 8.73 beats per second.
Beat ratios:
A2-C#3-F3 = 4.25 / 4.37 = 0.97.
C#3-F3-A3 = 8.50 / 4.25 = 2.00.
F3-A3-C#4 = 8.73 / 8.50 = 1.03.
In conclusion, A2-C#3 and C#3-F3 will beat as equally as possible and F3-A3 and A3-C#4 will beat as equally as possible.
------------------------------
Roshan Kakiya
Original Message:
Sent: 05-31-2019 22:39
From: Ed Sutton
Subject: A Request for Roshan Kakiya
Beats are the periodic rise and fall of amplitude that occur when two close, but not identical frequencies are played together. In the case of thirds they are the interference pattern between the fifth partial of the lower note and the fourth partial of the upper note. In ideal equal temperament beats of contiguous major thirds beat in a ratio of 4 to 5, the upper third being the "5."
In my process for assessing the tempering of a third, I intentionally lower the pitch of the top note of the lower pair of thirds until the interference patterns of the coincident partials of both thirds have identical periodicity.
My claim is that if the C#s are properly tempered for equal temperament, when one pair is altered to beat equally, the other pair will also beat equally. In this example the C#-F third beats slower than it would in equal temperament, and the F-A third beats faster.
------------------------------
Ed Sutton
ed440@me.com
(980) 254-7413
Original Message:
Sent: 05-31-2019 22:25
From: Roshan Kakiya
Subject: A Request for Roshan Kakiya
Dear Ed,
What is the meaning of equal beating?
Should A-C# and C#-F have the same beat rate?
Should F-A and A-C# have the same beat rate?
------------------------------
Roshan Kakiya
Original Message:
Sent: 05-31-2019 20:05
From: Ed Sutton
Subject: A Request for Roshan Kakiya
Dear Roshan,
O.K. and now we need to know
1) If A-C# = 400 cents and C#-F = 397.26 cents, and C# is the common tone of both thirds, are they equal beating?
and
2) If F-A = 402.74 cents and A-C# = 400 cents, and A is the common tone of both thirds, are they equal beating?
3) If not, what are the relative beat rates?
------------------------------
Ed Sutton
ed440@me.com
(980) 254-7413
Original Message:
Sent: 05-31-2019 19:34
From: Roshan Kakiya
Subject: A Request for Roshan Kakiya
Dear Ed,
Just Major Third = 1200 × log2(5/4) = 386.31 cents.
3 Consecutive Just Major Thirds = 1200 × log2(5/4 × 5/4 × 5/4) = 1200 × log2(125/64) = 1158.94 cents.
Equal-Tempered Major Third = 1200 × 4/12 = 400.00 cents.
3 Consecutive Equal-Tempered Major Thirds = 1200 × (4/12 + 4/12 + 4/12) = 1200 × 12/12 = 1200.00 cents.
Lesser Diesis = 1200 × log2(2/1 / 125/64) = 1200 × log2(2/1 × 64/125) = 1200 × log2(128/125) = 41.06 cents.
The Lesser Diesis is the difference between a Pure Octave and 3 Consecutive Just Major Thirds (1200.00 cents − 1158.94 cents) = 41.06 cents.
There are 3 Consecutive Just Major Thirds and 1 Lesser Diesis. Therefore, each of the 3 Just Major Thirds must be sharpened by 1/3 Lesser Diesis in order to remove the Lesser Diesis and ensure each of the 3 Consecutive Sharpened Major Thirds are the same in terms of size:
1/3 Lesser Diesis = 1200 × log2(128/125) / 3 = 13.69 cents.
Sharpened Major Third = 1200 × log2(5/4) + 1200 × log2(128/125) / 3 = 400.00 cents = Equal-Tempered Major Third.
3 Consecutive Equal-Tempered Major Thirds = 400.00 cents × 3 = 1200.00 cents.
"Contiguous equal-tempered Major Thirds beat at the ratio of 4:5, lower to upper third, each tempered by one-third of the diesis."
The calculations above indicate that sharpening a Just Major Third by 1/3 Lesser Diesis will lead to the creation of an Equal-Tempered Major Third.
"If I lower F3 to create equal-beating thirds A2-C#3-F3 (4:4) I have effectively removed one fifth of the one-third diesis from C#3-F3 and transferred it to F3-A3."
1/5 of 1/3 Lesser Diesis = 1/5 × 1200 × log2(128/125) / 3 = 2.74 cents.
A2-C#3 = 1200 × log2(5/4) + 1200 × log2(128/125) / 3 = 400.00 cents.
C#3-F3 = 1200 × log2(5/4) + 1200 × log2(128/125) / 3 − 1/5 × 1200 × log2(128/125) / 3 = 397.26 cents.
F3-A3 = 1200 × log2(5/4) + 1200 × log2(128/125) / 3 + 1/5 × 1200 × log2(128/125) / 3 = 402.74 cents.
"Thus, assuming correct octaves, the only division of a Major Tenth that will produce two pairs of equal-beating lower and upper contiguous Major Thirds requires that the lowest and highest Major Thirds are tempered to exactly one-third of the diesis.
Equal-Tempered Major Tenth = 1200 × 16/12 = 1600.00 cents.
A2-C#3-F3-A3 = 400.00 cents + 397.26 cents + 402.74 cents = 1200.00 cents.
A3-C#4 = 1600.00 cents − 1200.00 cents = 400.00 cents.
A2-C#3 = 400.00 cents = Just Major Third Sharpened by 1/3 Lesser Diesis.
C#3-F3 = 397.26 cents = Just Major Third Sharpened by 1/3 Lesser Diesis and Narrowed by 1/5 of 1/3 Lesser Diesis.
F3-A3 = 402.74 cents = Just Major Third Sharpened by 1/3 Lesser Diesis and Sharpened by 1/5 of 1/3 Lesser Diesis.
A3-C#4 = 400.00 cents = Just Major Third Sharpened by 1/3 Lesser Diesis.
------------------------------
Roshan Kakiya
Original Message:
Sent: 05-31-2019 15:09
From: Ed Sutton
Subject: A Request for Roshan Kakiya
Dear Roshan-
Perhaps you can help me with your mathematical skills.
In tuning pianos aurally, dividing an octave into three equally tempered Major Thirds is a highly effective way to begin. But it must begin with an estimate. Aural tuners get very good at making these first estimates, but it may be of value to have a technique that will quickly confirm the estimate. I recently devised a rule-of-thumb method that I'd not heard of previously. While it is useful in practice, I suspect it is not mathematically absolutely perfect.
In devising this technique I became very aware of the real, crude limits we face in tuning real pianos. For example how accurately can we tune or assess two "equal-beating" intervals? Can we really discern that one interval beats 50 times in 15 seconds and another beats 51 times in 15 seconds? In organ tuning, this could be done, but in piano tuning, it's highly unlikely! So, I think my thesis about Major Thirds works within the limits of hearing real world pianos but is probably a little off in absolute mathematics.
It seems likely you have the mathematical skills to do an accurate assessment. Would you please take a look and tell me what you think?
It's copied below and also attached.
Thank you!
Ed Sutton
An Aural Test for the Correct Estimate of an Equal-Tempered Major Third, as Used in Setting a Stack of Contiguous Major Thirds.
- Tune A4>A3>A2
- Tune A2>C#3, estimate at 4.3 bps
- Tune C#3>C#4
Here's the test:
- Tune C#3>F3 such that A2-C#3 and C#3-F3 are equal-beating.
- If F3-A3 are now-equal beating with A3-C#4, the C#s are correct for equal temperament, they are tempered at one third of the lesser diesis.
Proof:
- Contiguous equal-tempered Major Thirds beat at the ratio of 4:5, lower to upper third, each tempered by one-third of the diesis.
- If I lower F3 to create equal-beating thirds A2-C#3-F3 (4:4) I have effectively removed one fifth of the one-third diesisfrom C#3-F3 and transferred it to F3-A3.
Since F3-A3-C#4, correctly tuned beat at 4:5, transferring one-fifth of the one-third diesisproduces equal-beating contiguous thirds, changing the lower ratio from 4:5 to 4:4 and the upper pair ratio from 4:5 to 5:5.
Sequentially, the four thirds should beat 4:4:8:8
- If the C#s are too flat, the percentage of diesisto be divided by F3 will be too great, and one or both of the C#3-F3-A3 thirds will beat too fast relative to the too slow A-C# thirds.
- If the C#s are too sharp, the percentage of diesisto be divided by F3 will be too small, and one or both of the C#3-F3-A3 thirds will beat too slow relative to the too fast A-C# thirds.
- Thus, assuming correct octaves, the only division of a Major Tenth that will produce two pairs of equal-beating lower and upper contiguous Major Thirds requires that the lowest and highest Major Thirds are tempered to exactly one-third of the diesis. [This would also be true, for example, of F3-A3-C#4-F4-A4.]
Ed Sutton 5/6/2019
------------------------------
Ed Sutton
ed440@me.com
(980) 254-7413
------------------------------