Original Message:
Sent: 08-08-2025 21:08
From: Ron Koval
Subject: Equal Beating Temperament System
I'm just looking at the midrange octave or so now. If I can get numbers to match there, I'll let things fall where they may. I just loaded one Yamaha C3 to take a look and one of the midrange stretches matched the M3rd beats pretty well from Jason's chart and I got about 1/2 of an octave with 1bps for the 5ths so I would go with that stretch if I was going to tune it. This was my first look with your posted tuning offsets.
Ron Koval
------------------------------
Ron Koval
CHICAGO IL
Original Message:
Sent: 08-08-2025 18:30
From: Roshan Kakiya
Subject: Equal Beating Temperament System
Hi Ron,
In order to maintain the same beat rates across the entirety of the keyboard, something has to give way. In my case, wolf 5ths are emerging. 12-EBT is adjusting itself to account for the wolf 5ths by either doubling the beat rate of each 5th and 4th within each successive octave as you go upwards or halving the beat rate of each 5th and 4th within each successive octave as you go downwards. It is automatically tempering out some sort of "comma" to maintain the integrity of its design across the entirety of the keyboard.
The principles of the Equal Beating Temperament System are working with each other as much as they are working against each other.
Have you managed to reconcile the discrepancies that arise as a result of the linear nature of beat rates and the logarithmic nature of pitch progression?
That is the ultimate question.
------------------------------
Roshan Kakiya
------------------------------
Original Message:
Sent: 08-08-2025 16:23
From: Ron Koval
Subject: Equal Beating Temperament System
Very mild temperaments are where I've practiced for a number of decades now, so I'm following along here.
One piece of new data to me is that the application of any of these offsets to move from an EDT ET calculation to an alternate temperament may not result in the interval beat speeds that we had hoped to see. Not only inharmonicity of the piano, but the specific octave width used in the midrange will have significant effect on the beats. I've seen this using the beta version of PiaTune which is an iOS app. It is possible to display a chart of midrange M3rds and 5ths while choosing the stretch and temperament choice. I've found a number of temperaments need to have all offsets divided to achieve close to the desired beats or reaching near equal beating of indicated intervals. If anyone else is interested in looking into this send an email to support@piatune.com to get an invite to the beta. Hakki is the name of the developer and is very responsive to input from technicians.
Tim Foster has shared some new very mild temperaments as well.
Ron Koval
------------------------------
Ron Koval
CHICAGO IL
Original Message:
Sent: 08-08-2025 11:59
From: Roshan Kakiya
Subject: Equal Beating Temperament System
Hi Jason,
It seems as though this problem will occur regardless of which temperament is being used. I plugged the offsets that I have calculated for the Equal Beating Victorian Temperament into my spreadsheet for 12-EBT, then I extended the temperament. The beat rates doubled in the Octave A4-A5, then they quadrupled in the Octave A5-A6.
The equation for 12-EBT is automatically adapting to the offsets. The Octave A4-A5 has a new equation with a new solution.
Equation for Octave A4-A5: ((((((((((((((((((((((((880 × 2 + Δ) / 3) × 4 + Δ) / 3) × 2 + Δ) / 3) × 4 + Δ) / 3) × 2 + Δ) / 3) × 4 + Δ) / 3) × 4 + Δ) / 3) × 2 + Δ) / 3) × 4 + Δ) / 3) × 2 + Δ) / 3) × 4 + Δ) / 3) × 2 + Δ) / 3) = 440
Solution: 3147320 / 1568693
What is 1573660 / 1568693 = 1.003166330? It is the beat rate in Hz of the 5ths and the 4ths within the Octave A3-A4 in 12-EBT. What is 3147320 / 1568693 = 2.006332660? It is the beat rate in Hz of the 5ths and the 4ths within the Octave A4-A5 in 12-EBT.
The numerator has doubled (3147320 / 1573660 = 2). I tried to maintain the original ratio (1573660 / 1568693) across every octave, but I ended up with wolf 5ths. 12-EBT appears to be adjusting its own design automatically to temper out some sort of "comma".
A similar problem occurs in equal temperament. I explored the design of Pure 26th Equal Temperament in the past: https://my.ptg.org/communities/community-home/digestviewer/viewthread?GroupId=43&MessageKey=d473dba2-70e9-4d3a-ab5a-30b6a8cbf24f&CommunityKey=6265a40b-9fd2-4152-a628-bd7c7d770cbf. What is the discrepancy between 12 Pure 5ths and 7 Pure Octaves? The Pythagorean Comma = 23.46 cents. What is the discrepancy between 24 Pure 12ths and 19 Pure Double Octaves? The Double Pythagorean Comma = 46.92 cents. The Pure Octave (1200 cents) has been doubled to form the Pure Double Octave (2400 cents), and the Pythagorean Comma has doubled (46.92 cents / 23.46 cents = 2).
The harmonic series exhibits "natural inharmonicity". Harmonic partials are travelling at different rates even before "real inharmonicity" is taken into consideration. At 440 Hz, a 1 Hz change at the 1st partial level (441 Hz) will cause a 2 Hz change at the 2nd partial level (882 Hz), a 3 Hz change at the 3rd partial level (1323 Hz), a 4 Hz change at the 4th partial level (1764 Hz), and so on. "Real inharmonicity" modifies the "natural inharmonicity" that is already present in the harmonic series. "Natural inharmonicity" can be accounted for via beat rate distribution ratios, which distribute beat rates across partials. "Real inharmonicity" modifies those ratios. They are found in the harmonic series itself. The relationship between the 1st and 2nd partials is 1 : 2 (Ratios: 1 / 3 for the 1st partial and 2 / 3 for the 2nd partial). The relationship between the 2nd and 3rd partials is 2 : 3 (Ratios: 2 / 5 for the 2nd partial and 3 / 5 for the 3rd partial). The relationship between the 3rd and 4th partials is 3 : 4 (Ratios: 3 / 7 for the 3rd partial and 4 / 7 for the 4th partial). The relationship between the 4th and 5th partials is 4 : 5 (Ratios: 4 / 9 for the 4th partial and 5 / 9 for the 5th partial). The relationship between the 5th and 6th partials is 5 : 6 (Ratios: 5 / 11 for the 5th partial and 6 / 11 for the 6th partial). The list goes on. Those ratios enable us to produce equally beating intervals. However, the various "commas" still have to be tempered out because they keep popping up everywhere. 12-EBT is tempering out a "comma" automatically by doubling its beat rates from one octave to another. If the beat rates are not doubled from one octave to another, wolf 5ths emerge.
Something has to give way somewhere.
------------------------------
Roshan Kakiya
------------------------------
Original Message:
Sent: 08-07-2025 17:26
From: Jason Kanter
Subject: Equal Beating Temperament System
I fed the temperament offsets into my Unequal Temperament spreadsheet, which charts the C3-C4 octave, and here's what it looks like:
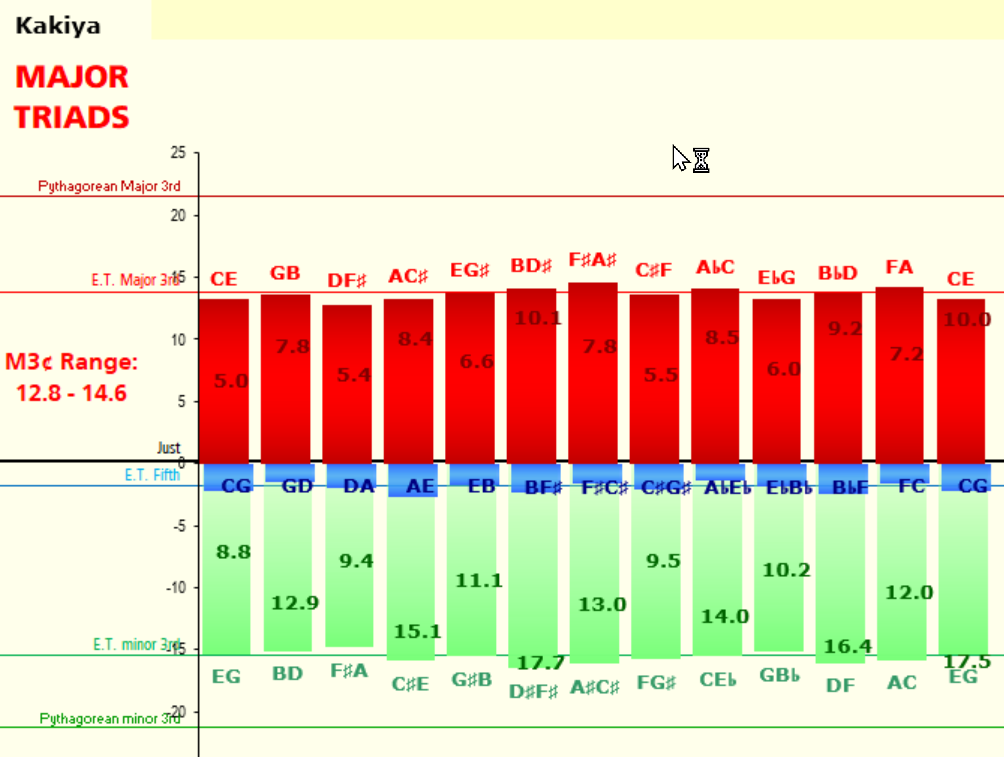
And here is the data for each data point in the chart:
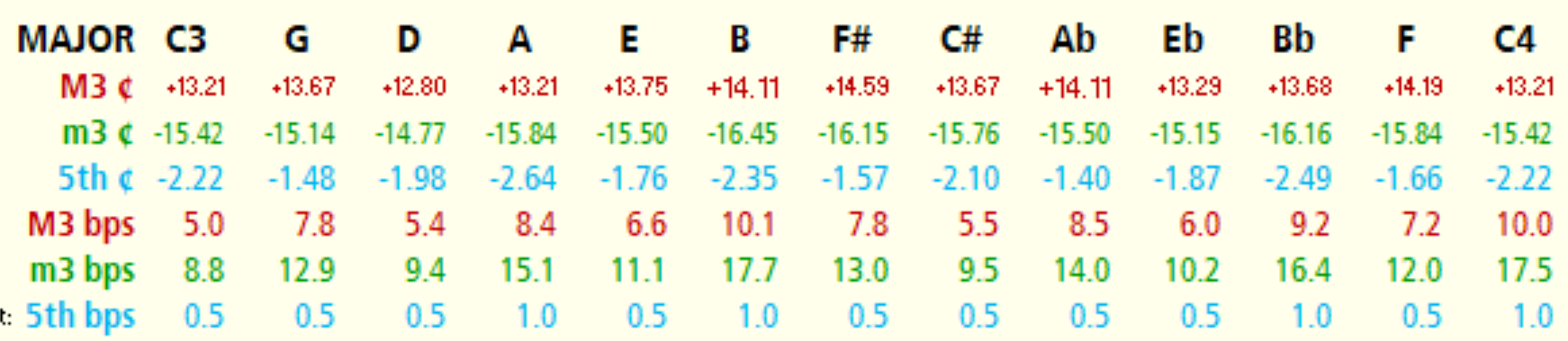If you look at the bottom line of data, the beat speed of the 5ths, you'll notice that each note from A3 to Ab3 has a 5th that beats at 0.5 bps ... and from A3 to C4 they all beat at 1.0 bps. So Roshan's math makes equal-beating fifths only in the range A3-A4. The next octave up all the fifths will beat at 2.0 bps, and the next octave beyond that will have fifths beating at 4.0 bps.
Maybe this is fine. Just saying.
------------------------------
| || ||| || ||| || ||| || ||| || ||| || ||| || |||
Jason Kanter
Lynnwood WA
(425) 830-1561
Original Message:
Sent: 08-06-2025 23:02
From: Peter Grey
Subject: Equal Beating Temperament System
I'm now wondering if Silver and Feaster knew each other (the wording in Feaster's book is eerily similar to that of Silver's description), or worse...if one "copied" the other. Feaster claims he'd been using this for quite some time before actually writing his book. Interesting, though AFAIK he does not actually lay claim to having originated it.
Peter Grey Piano Doctor
------------------------------
Peter Grey
Stratham NH
(603) 686-2395
pianodoctor57@gmail.com
Original Message:
Sent: 08-06-2025 21:10
From: Roshan Kakiya
Subject: Equal Beating Temperament System
Hi David,
I appreciate your comments, but I have posted my research on the Equal Beating Victorian Temperament (EBVT), which is an unequal temperament, as well as my research on the Pure Octave Equal Beating Temperament (12-EBT), which is also an unequal temperament. EBVT is closer to unequal temperament, whereas 12-EBT is closer to equal temperament. I have accounted for both ends of the spectrum. At the end of the day, they are both equal-beating temperaments. There is absolutely nothing about equal temperament here. It is all about equal beating!
------------------------------
Roshan Kakiya
------------------------------
Original Message:
Sent: 08-06-2025 20:49
From: David Pinnegar
Subject: Equal Beating Temperament System
Dear Roshan
" the production of equally beating intervals seems to be holy grail of piano tuning"
Actually no. This is an assumption and one which is arguably faulty. The holy grail of tuning pianos should be to best enable the expression of the music. Equal or quasi equal temperament puts a high speed motorway through the landmarks of modulation and the narrative of the music.
In the country of Georgia between Tbilisi and Kudaisi there is a range of mountains over and through which the main road passes. It's very picturesque. The Chinese have, at great expense and environmental destruction, forced through a motorway through mountains and over bridges through valleys. The traffic will rush through, the passengers not appreciate the realities of the landscape even if they can see it on a transitory basis - they won't feel it - and all the businesses and stopping points along the old road will starve and die. This is what the equal temperament has done to performance in the tuning systems of the 20th century.
Best wishes
David P
--
- - - - - - - - - - - - - - - - - - - - - - - -
David Pinnegar, B.Sc., A.R.C.S.
- - - - - - - - - - - - - - - - - - - - - - - -
+44 1342 850594
Original Message:
Sent: 8/6/2025 8:00:00 PM
From: Roshan Kakiya
Subject: RE: Equal Beating Temperament System
Hi Peter,
Thank you for engaging with me so actively. I enjoy reading your messages.
I reckon that the Pure Octave Equal Beating Temperament (12-EBT) is exactly the same as the Equal Beating Chromatic Scale by A. L. Leigh Silver, which was published in the 1950s in Volume 29, Issue 4 of the Journal of the Acoustical Society of America (JASA).
Here is the content that is available at https://pubs.aip.org/asa/jasa/article-abstract/29/4/476/720902/Equal-Beating-Chromatic-Scale:
"An unequal temperament is described in which the fifths and fourths of the tuning chain have the same beat rate. No Wolf intervals are produced and all intervals can be described by ratios of integers. The equal heating chromatic scale is an excellent approximation to equal temperament; moreover it may well represent a closer approximation to Bach's "well‐tempered tuning" than does equal temperament. Circulation of a kind is complete and this tends to restore in some degree the feature of key color. Inasmuch as there is only one beat rate to observe (very nearly one per second) the procedure for tuning keyboard instruments to this temperament is simpler than that nominally required for equal temperament. Tuning notes are appended."
Unfortunately, I do not have access to the rest of the content, so I have decided to create my own version of this temperament instead. I have done my own research on the Equal Beating Temperament System because such limited information is available about it. It is fascinating to know that other publications for equal-beating temperaments exist. Owen Jorgensen has published information about them, but I have not managed to get my hands on his books. Thank you for making me aware of C. Raymond Feaster's work. From my perspective, the only readily accessible theoretical model is Alfredo Capurso's Circular Harmonic System, and the only readily accessible practical model is Bill Bremmer's Equal Beating Victorian Temperament. I am strictly adhering to the production of equally beating intervals for my research in order to remain faithful to the Equal Beating Temperament System, so I have ruled out any temperaments that have unequally beating intervals in their sequence.
I was reading an interesting discussion about tuning pipe organs via equally beating 5ths and 4ths a while ago at https://www.reddit.com/r/microtonal/comments/bxvfx5/equal_beating_temperament. I highly respect the hard work that the people there have put in to finding a "recipe", but their work falls short of my standards. Therefore, I have designed a proper 12-EBT that makes 5ths and 4ths beat equally within a pure octave to the highest possible level of accuracy by creating one single equation for the whole thing. That is what you call a "recipe"!
I have reached the end of the road in terms of mathematically exploring the theory of tuning because the production of equally beating intervals seems to be the holy grail of piano tuning. Everything about piano tuning made sense to me once I dedicated myself to researching equally beating intervals. I must admit, I had to use all of my research into the mathematics of tuning up to this point to wrap my head around how they work, so it was all time well spent. I have reached the pinnacle of my research now. I honestly cannot think of where I can go from here. This is it.
🙂
------------------------------
Roshan Kakiya
------------------------------
Original Message:
Sent: 08-06-2025 18:27
From: Peter Grey
Subject: Equal Beating Temperament System
Roshan,
Now that I see it, it turns out that this is essentially identical to what C. Raymond Feaster published back in 1958 in his book: "The Dynamic Scale and How To Tune It".
It's a hard book to find but I obtained a hard copy years ago. However I was first exposed to it by the late Orman D. Pratt, RPT of the DC Chapter PTG back in 1978 B or so. So...evidently it ain't new 🤔
Peter Grey Piano Doctor
------------------------------
Peter Grey
Stratham NH
(603) 686-2395
pianodoctor57@gmail.com
Original Message:
Sent: 08-04-2025 00:00
From: Roshan Kakiya
Subject: Equal Beating Temperament System
Equal Beating Temperament System
Principles
To account for the linear nature of beat rates, add and subtract the frequencies of coincident partials.
To account for the logarithmic nature of pitch perception, multiply and divide the frequencies of non-coincident partials.
Theory
Alfredo Capurso's Circular Harmonic System:
https://www.scribd.com/document/174787881/Alfredo-Capurso-A-New-Model-of-Interpretation-of-Some-Acoustic-Phenomena-Circular-Harmonic-System-C-HA-S
Practice
Bill Bremmer's Equal Beating Victorian Temperament:
https://billbremmer.com/ebvt
Research
Roshan Kakiya's Final Discussion Thread:
https://my.ptg.org/discussion/final-discussion-thread-circular-harmonic-system-for-equally-beating-intervals
Files
- Circular Harmonic System
- Circular Harmonic System Equations for Equally Beating 12th and 15th
- Beat Rate Analysis of Circular Harmonic System Equations for Equally Beating 12th and 15th
- Beat Rate Analysis of Circular Harmonic System Equations for Equally Beating 5th and 4th
- Equal Beating Victorian Temperament
- Analysis of Equal Beating Victorian Temperament
- Illustration: Equally Beating Upper Note Common 5th A3-E4 and 4th B3-E4 without Inharmonicity in Equal Beating Victorian Temperament
- Illustration: Equally Beating Upper Note Common 5th A3-E4 and 4th B3-E4 with Inharmonicity in Equal Beating Victorian Temperament
- Equal Beating Temperament System
- Scala File for Equal Beating Victorian Temperament
------------------------------
Roshan Kakiya
------------------------------